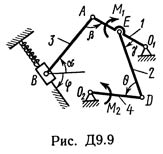
Solution D9-93 (Figure D9.9 condition 3 SM Targ 1989)
If the total amount of your purchases from the seller Михаил_Перович more than:
- 200 $ the discount is 15%
- 100 $ the discount is 10%
- 50 $ the discount is 7%
- 20 $ the discount is 5%
- 10 $ the discount is 3%
- 5 $ the discount is 2%
- 1 $ the discount is 1%
Sold 1
Refunds 0
Good feedbacks 0
Bad feedbacks 0
Solution D9-93 (Figure D9.9 condition 3 SM Targ 1989)
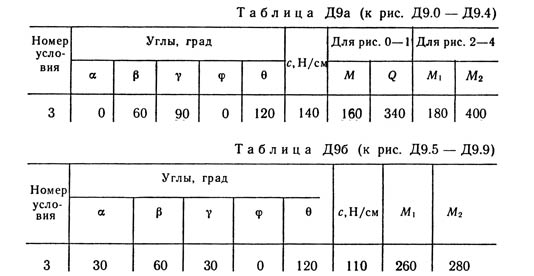
The mechanism located in the horizontal plane is under the action of the applied forces in equilibrium; the equilibrium position is determined by the angles α, β, γ, φ, θ (Fig. D9.0-D9.9, Tables D9a and D9b). The lengths of the rods of the mechanism (cranks) are: l1 = 0.4 m, l4 = 0.6 m (dimensions l2 and l3 are arbitrary); Point E is in the middle of the corresponding rod. The elasticity of the spring F acts on the slider B of the mechanism; numerically F = cλ, where c is the spring stiffness coefficient, λ is its deformation. In addition, in Fig. 0 and 1 the force Q acts on the slider D, and on the crank O1A - a pair of forces with the moment M; in Fig. 2-9, the pairs of forces with moments M1 and M2 act on the cranks O1A and O2D. Determine what is equal to the deformation of the spring at equilibrium, and indicate whether the spring is stretched or compressed. The values of all given values are given in Table. A9a for Fig. 0-4 and in Table. D9b for Fig. 5-9, where Q is expressed in newtons, and M, M1, M2 - in newtonometers. Draw a drawing from the rod, the direction of which is determined by the angle α; For greater clarity, the slider with the guides and the spring is shown in the same way as in Example D9 (see Figure D9, as well as Figure D9.10, b). If, in the figure of the solved variant of the problem, the rod attached to the slider B is aligned with the spring (as in Figure D9.10, a), the spring should be considered attached to the slider on the other side (as in Figure D9.10, b, where simultaneously otherwise the guides are shown).
The mechanism located in the horizontal plane is under the action of the applied forces in equilibrium; the equilibrium position is determined by the angles α, β, γ, φ, θ (Fig. D9.0-D9.9, Tables D9a and D9b). The lengths of the rods of the mechanism (cranks) are: l1 = 0.4 m, l4 = 0.6 m (dimensions l2 and l3 are arbitrary); Point E is in the middle of the corresponding rod. The elasticity of the spring F acts on the slider B of the mechanism; numerically F = cλ, where c is the spring stiffness coefficient, λ is its deformation. In addition, in Fig. 0 and 1 the force Q acts on the slider D, and on the crank O1A - a pair of forces with the moment M; in Fig. 2-9, the pairs of forces with moments M1 and M2 act on the cranks O1A and O2D. Determine what is equal to the deformation of the spring at equilibrium, and indicate whether the spring is stretched or compressed. The values of all given values are given in Table. A9a for Fig. 0-4 and in Table. D9b for Fig. 5-9, where Q is expressed in newtons, and M, M1, M2 - in newtonometers. Draw a drawing from the rod, the direction of which is determined by the angle α; For greater clarity, the slider with the guides and the spring is shown in the same way as in Example D9 (see Figure D9, as well as Figure D9.10, b). If, in the figure of the solved variant of the problem, the rod attached to the slider B is aligned with the spring (as in Figure D9.10, a), the spring should be considered attached to the slider on the other side (as in Figure D9.10, b, where simultaneously otherwise the guides are shown).