Solution D5-55 (Figure D5.5 condition 5 SM Targ 1989)
If the total amount of your purchases from the seller Михаил_Перович more than:
- 200 $ the discount is 15%
- 100 $ the discount is 10%
- 50 $ the discount is 7%
- 20 $ the discount is 5%
- 10 $ the discount is 3%
- 5 $ the discount is 2%
- 1 $ the discount is 1%
Sold 1
Refunds 0
Good feedbacks 0
Bad feedbacks 0
Solution D5-55 (Figure D5.5 condition 5 SM Targ 1989)
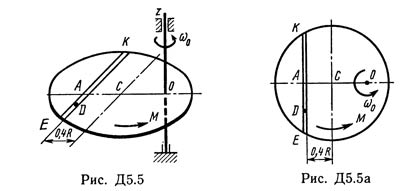
A uniform horizontal platform (of circular radius R or rectangular with sides R and 2R, where R = 1.2 m) with mass m1 = 24 kg rotates with angular velocity ω0 = 10 s-1 around the vertical axis z, away from the center of mass C of the platform on distance OC = b (Fig. D5.0-D5.9, Table D5); The dimensions for all rectangular platforms are shown in Fig. D5.0a (top view). At the time t0 = 0, a load D of mass m2 = 8 kg starts to move along the platform trench according to the law s = AD = F (t) where s is expressed in meters, t - in seconds. At the same time, a pair of forces with a moment M starts to act on the platforms (specified in newtonometers, for M <0 its direction is opposite to that shown in the figures). Determine, by neglecting the shaft mass, the dependence ω = f (t), i.e., the angular velocity of the platform, as a function of time. In all figures, the load D is shown at a position at which s> 0 (when s <0, the load is on the other side of point A). Drawing the drawing of the problem being solved, draw the z-axis at a given distance OC = b from the center of C.
A uniform horizontal platform (of circular radius R or rectangular with sides R and 2R, where R = 1.2 m) with mass m1 = 24 kg rotates with angular velocity ω0 = 10 s-1 around the vertical axis z, away from the center of mass C of the platform on distance OC = b (Fig. D5.0-D5.9, Table D5); The dimensions for all rectangular platforms are shown in Fig. D5.0a (top view). At the time t0 = 0, a load D of mass m2 = 8 kg starts to move along the platform trench according to the law s = AD = F (t) where s is expressed in meters, t - in seconds. At the same time, a pair of forces with a moment M starts to act on the platforms (specified in newtonometers, for M <0 its direction is opposite to that shown in the figures). Determine, by neglecting the shaft mass, the dependence ω = f (t), i.e., the angular velocity of the platform, as a function of time. In all figures, the load D is shown at a position at which s> 0 (when s <0, the load is on the other side of point A). Drawing the drawing of the problem being solved, draw the z-axis at a given distance OC = b from the center of C.