Solution D12-61 (Figure D12.6 condition 1 SM Targ 1989)
If the total amount of your purchases from the seller Михаил_Перович more than:
- 200 $ the discount is 15%
- 100 $ the discount is 10%
- 50 $ the discount is 7%
- 20 $ the discount is 5%
- 10 $ the discount is 3%
- 5 $ the discount is 2%
- 1 $ the discount is 1%
Sold 1
Refunds 0
Good feedbacks 0
Bad feedbacks 0
Solution D12-61 (Figure D12.6 condition 1 SM Targ 1989)
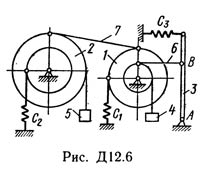
The mechanism located in the vertical plane (Fig. D12.0 - D12.9) consists of stepped wheels 1 and 2 with radii R1 = 0.4 m, r1 = 0.2 m, R2 = 0.5 m, r2 = 0.3 m, having fixed axis of rotation; a homogeneous rod 3 of length l = 1.2 m, fixed by a hinge at one of the ends; cargo 4 and 5, suspended to the threads wound on the wheels. On the rod, the distance AB = 2l / 3. The rod 3 is connected to the wheel 2 by a weightless rod 6. The wheels 1 and 2 are either meshed (Figure 0-4), or connected by a weightless rod 7 (Figure 5-9). The springs are attached to the wheels and the rod 3. In Table. D12 are the masses mi of bodies (kg) and the stiffness coefficients ci of the springs (N / m). The dashes in the columns of the table mean that the corresponding bodies or springs do not enter the system (in the drawing, these bodies and springs are not represented); as a result, in each specific variant, a fairly simple mechanism is obtained, containing three or even two bodies. Rod 6 or 7 is part of the mechanism, when it includes both bodies connected by this rod. In the positions depicted in the figures, the mechanism is in equilibrium. Determine the frequency and period of small oscillations of the system near the equilibrium position. Find also what is the static elongation (compression) of the spring λst in the equilibrium position. When counting, consider wheels 1 and 2 as solid, uniform cylinders of radii R1 and R2, respectively. Let us consider two examples of solving this problem.
The mechanism located in the vertical plane (Fig. D12.0 - D12.9) consists of stepped wheels 1 and 2 with radii R1 = 0.4 m, r1 = 0.2 m, R2 = 0.5 m, r2 = 0.3 m, having fixed axis of rotation; a homogeneous rod 3 of length l = 1.2 m, fixed by a hinge at one of the ends; cargo 4 and 5, suspended to the threads wound on the wheels. On the rod, the distance AB = 2l / 3. The rod 3 is connected to the wheel 2 by a weightless rod 6. The wheels 1 and 2 are either meshed (Figure 0-4), or connected by a weightless rod 7 (Figure 5-9). The springs are attached to the wheels and the rod 3. In Table. D12 are the masses mi of bodies (kg) and the stiffness coefficients ci of the springs (N / m). The dashes in the columns of the table mean that the corresponding bodies or springs do not enter the system (in the drawing, these bodies and springs are not represented); as a result, in each specific variant, a fairly simple mechanism is obtained, containing three or even two bodies. Rod 6 or 7 is part of the mechanism, when it includes both bodies connected by this rod. In the positions depicted in the figures, the mechanism is in equilibrium. Determine the frequency and period of small oscillations of the system near the equilibrium position. Find also what is the static elongation (compression) of the spring λst in the equilibrium position. When counting, consider wheels 1 and 2 as solid, uniform cylinders of radii R1 and R2, respectively. Let us consider two examples of solving this problem.