Solution D11-02 (Figure D11.0 condition 2 SM Targ 1989)
If the total amount of your purchases from the seller Михаил_Перович more than:
- 200 $ the discount is 15%
- 100 $ the discount is 10%
- 50 $ the discount is 7%
- 20 $ the discount is 5%
- 10 $ the discount is 3%
- 5 $ the discount is 2%
- 1 $ the discount is 1%
Sold 1
Refunds 0
Good feedbacks 0
Bad feedbacks 0
Solution D11-02 (Figure D11.0 condition 2 SM Targ 1989)
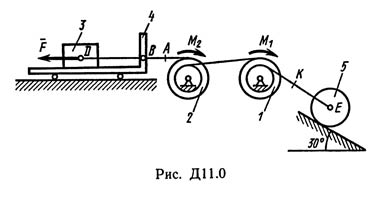
The mechanical system consists of bodies 1, 2, ..., 5 with weights P1, P2, ..., P5, respectively, connected with each other by yarns wound on step blocks 1 and 2 (Figure D11.0-D11.9, Table D11) . The radii of step blocks 1 and 2 are respectively R1 = R, r1 = 0.4R, R2 = R, r2 = 0.8R. When calculating the moments of inertia, all blocks, rollers and wheels are assumed to be homogeneous solid cylinders of radius R. On the system, in addition to the forces of gravity, the force F applied to the body 3 or 4 acts (if the body 3 does not enter the system, force is applied at point B to the trolley) and pairs of forces with moments M1, M2, applied to blocks 1 and 2; when M <0, the direction of the moment is opposite to that shown in the figure. In the section of the thread indicated in the table in the column "Spring", a spring with a stiffness coefficient c is included (for example, if the column is AB, then the section AB is a spring, if AD, then AD is a spring, etc.); At the initial time, the spring is not deformed. Write for the system the Lagrangian equation and find the law of variation of the generalized coordinate x, that is, x = f (t), assuming that the motion starts from a state of rest; determine also the frequency and period of oscillations made by the bodies of the system as it moves (for the choice of the coordinate x, see "Instructions"). A dash in the columns of the table, where the weights are specified, means that the corresponding body does not enter the system (not to depict in the drawing), but zero - that the body is weightless, but enters the system; for the wheels numbered 4, P4 - their total weight (the weight of the platform of such a trolley is not taken into account).
The mechanical system consists of bodies 1, 2, ..., 5 with weights P1, P2, ..., P5, respectively, connected with each other by yarns wound on step blocks 1 and 2 (Figure D11.0-D11.9, Table D11) . The radii of step blocks 1 and 2 are respectively R1 = R, r1 = 0.4R, R2 = R, r2 = 0.8R. When calculating the moments of inertia, all blocks, rollers and wheels are assumed to be homogeneous solid cylinders of radius R. On the system, in addition to the forces of gravity, the force F applied to the body 3 or 4 acts (if the body 3 does not enter the system, force is applied at point B to the trolley) and pairs of forces with moments M1, M2, applied to blocks 1 and 2; when M <0, the direction of the moment is opposite to that shown in the figure. In the section of the thread indicated in the table in the column "Spring", a spring with a stiffness coefficient c is included (for example, if the column is AB, then the section AB is a spring, if AD, then AD is a spring, etc.); At the initial time, the spring is not deformed. Write for the system the Lagrangian equation and find the law of variation of the generalized coordinate x, that is, x = f (t), assuming that the motion starts from a state of rest; determine also the frequency and period of oscillations made by the bodies of the system as it moves (for the choice of the coordinate x, see "Instructions"). A dash in the columns of the table, where the weights are specified, means that the corresponding body does not enter the system (not to depict in the drawing), but zero - that the body is weightless, but enters the system; for the wheels numbered 4, P4 - their total weight (the weight of the platform of such a trolley is not taken into account).